前言
在学习 PyTorch 的过程中,发现资料里面经常提到乘法、点积( *、 mul()、multiply()、mm()、bmm()、mv()、dot()、matmul()、@)等等,总是傻傻的弄不清,总是不明白资料里面的结果是如何计算出来的,于是就找点资料研究一下,这里做一下记录。
对位相乘(mul 、multiply 、*)
mul 、multiply 、*,这三者效果是一样的。官网上明确说明,multiply是mul的别名。对应位相乘,支持广播。支持数字或张量
1
2
3
4
5
6
7
8
import torch
a = torch.tensor([[1,2,3],[4,5,6]])
b = torch.tensor([[7,8,9],[10,11,12]])
a*b
torch.mul(a,b)
torch.multiply(a,b)
# [[1,2,3],[4,5,6]] * [[7,8,9],[10,11,12]] = [[ 1*7 , 2*8 , 3*9 ],[ 4*10 , 5*11 , 6*12 ]] = [[ 7,16,27],[40,55,72]]
矩阵乘法(mm、bmm)
mm是矩阵乘法,bmm是批量矩阵乘法,不广播。
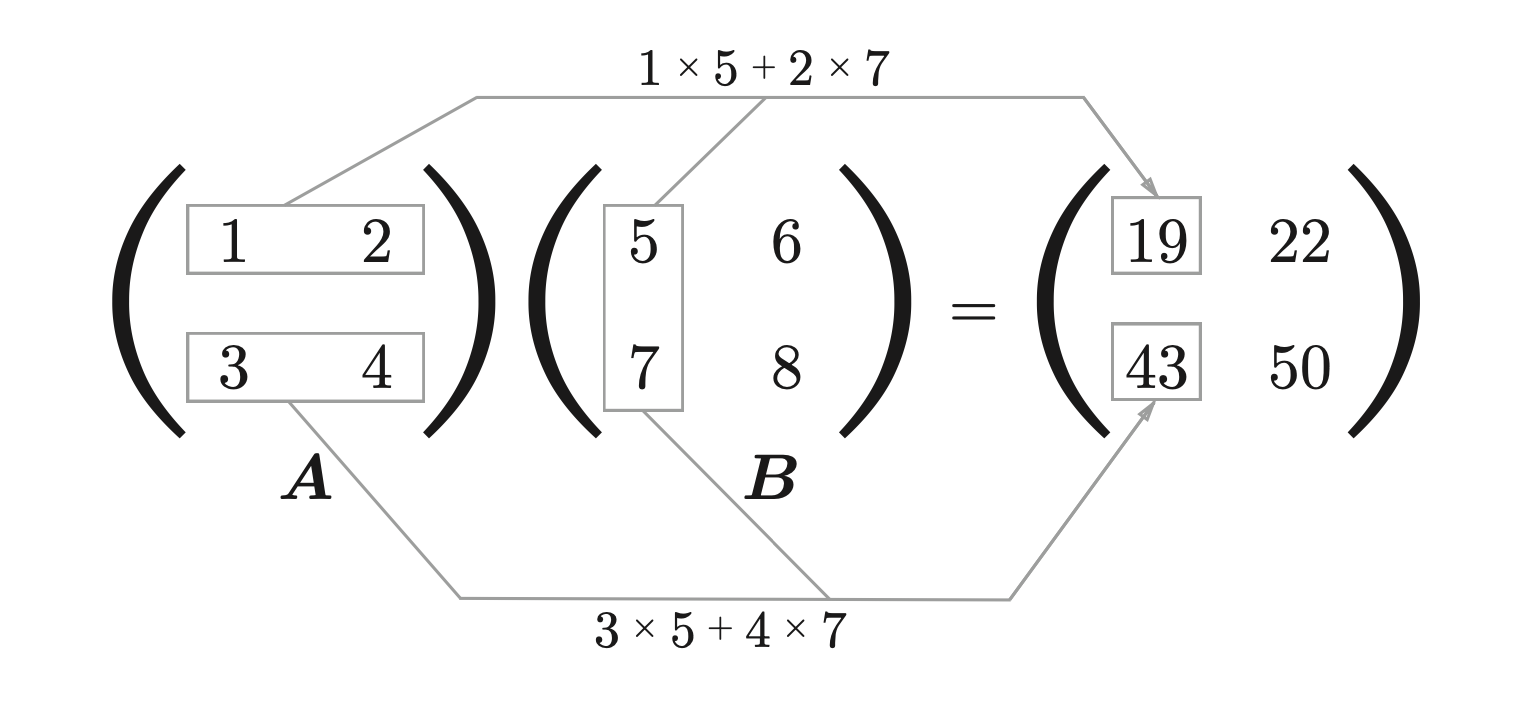
矩阵乘法是将第一个矩阵的第一行与第二个矩阵的第一列相乘并把结果相加,得到结果的第一行第一列的元素,然后再将第一个矩阵的第一行与第二个矩阵的第二列相乘并把结果相加,得到结果的第一行第二列的元素, 以此类推。
[n,m] x [m,p] = [n,p]
bmm是mm的批量操作,mm是矩阵乘法,是二维操作,但是实际工作中我们经常是批量计算的,所有就有了bmm。bmm是三维的,第一个维度是批量数。如:一张单通道图片是[25,25]的矩阵,如果一次处理十张就是[10,25,25],
bmm就是[10,25,25]的计算,也就是10个mm计算的结果
参数必须为矩阵,且需要符合第一个矩阵的行的元素数(列数)等于第二个矩阵的列的元素数(行数)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import torch
a = torch.tensor([[1,2,3],[4,5,6]])
b = torch.tensor([[7,8,9,10],[11,12,13,14],[15,16,17,18]])
torch.mm(a,b)
# tensor([[ 74, 80, 86, 92],[173, 188, 203, 218]])
# [
# [
# 74 = 1*7+2*11+3*15
# 80 = 1*8+2*12+3*16
# 86 = 1*9+2*13+3*17
# 92 = 1*10+2*14+3*18
# ],[
# 173 = 4*7+5*11+6*15
# 188 = 4*8+5*12+6*16
# 203 = 4*9+5*13+6*17
# 218 = 4*10+5*14+6*18
# ]
# ]
矩阵与向量相乘(mv)
矩阵与向量相乘,不广播。矩阵的第一行与向量的对应位相乘,结果相加,得到第一个元素,矩阵的第二行与向量的对应位相乘,结果相加,得到第二个元素,以此类推,要求矩阵的列与向量的元素个数相同。
第一个参数必须是矩阵,第二个参数必须是向量,且第一个矩阵的列数必须等于第二个向量元素个数。文档上说结果是张量,觉得更具体应该向量,且元素数是第一个矩阵的行数。
1
2
3
4
5
6
7
import torch
a = torch.tensor([[1,2],[3,4]])
b = torch.tensor([5,6])
torch.mv(a,b)
# tensor([17, 39])
# [17 = 1*5+2*6, 39 = 3*5+4*6]
点积(dot)
计算两个一维张量的点积。不广播。
注:与 NumPy 的 dot 不同,torch.dot 仅支持计算两个具有相同数量元素的 1D 张量的点积。不支持多维张量。
点积在数学中,又称数量积(dot product; scalar product),是指接受在实数R上的两个向量并返回一个实数值标量的二元运算。它是欧几里得空间的标准内积。
1
2
3
4
5
6
import torch
a = torch.tensor([1,2])
b = torch.tensor([3,4])
torch.dot(a,b)
# tensor(11)
# 1*3+2*4 = 11
张量的矩阵积(matmul 、@)
matmul 、@两个是等价的,用于计算张量的矩阵积。广播。这个是一个很复杂的操作,为什么这么说呢,就连文档上的说明都很复杂。简单来理解就是torch.dot() + torch.mv() + torch.mm() + torch.bmm()。如果这样理解,那就会很简单。
他的参数是两个张量。先说一种情况:
1、两个张量都是二维的,那么就是矩阵乘法。好巧这不就是mm吗?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
a = torch.tensor([[1,2],[3,4],[5,6]])
b = torch.tensor([[7,8,9],[10,11,12]])
torch.matmul(a,b)
# tensor([[ 27, 30, 33],[ 61, 68, 75],[ 95, 106, 117]])
# 27 = 1*7+2*10
# 30 = 1*8+2*11
# 33 = 1*9+2*12
# 61 = 3*7+4*10
# 68 = 3*8+4*11
# 75 = 3*9+4*12
# 95 = 5*7+6*10
# 106 = 5*8+6*11
# 117 = 5*9+6*12
2、两个张量都是一维的,那么就是向量与向量的点积。好巧,这不就是dot吗?
1
2
3
4
5
a = torch.tensor([1,2,3])
b = torch.tensor([7,8,9])
torch.matmul(a,b)
# tensor(50)
# 50 = 1*7+2*8+3*9
3、两个张量一个是二维的一个是一维的。好巧,这不就是mv吗?
1
2
3
4
5
6
a = torch.tensor([[1,2,3],[4,5,6]])
b = torch.tensor([7,8,9])
torch.matmul(a,b)
# tensor([ 50, 122])
# 50 = 1*7+2*8+3*9
# 122 = 4*7+5*8+6*9
4、高维张量,就是批量的矩阵乘法,好巧,这不就是bmm吗?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
a=torch.randn(2,3,4,5)
# tensor([[[[-1.0527, -0.1027, 1.5271, -1.1164, -0.9572],
# [-2.0193, 0.3352, -0.9644, 0.8497, -1.1244],
# [ 0.9561, -0.0916, -0.1582, -0.4133, 3.2017],
# [-0.4621, 0.2617, -1.2411, 0.5245, 0.0912]],
# [[ 1.7885, -1.4297, -1.8231, -0.6999, 0.0912],
# [-0.8359, 1.1325, 0.6162, 0.6178, 0.4088],
# [ 0.3157, 1.4147, -0.4691, -0.9922, 0.7739],
# [ 0.7214, -0.7779, 1.8310, 1.1669, 0.4956]],
# [[-0.9476, 2.0869, 0.2119, 0.5859, -0.5436],
# [ 0.8571, -0.1194, -0.1486, 1.0368, -1.2995],
# [-0.0950, 0.5803, 0.4826, -1.3057, -0.9637],
# [-1.0336, -0.8623, -0.5787, 1.7596, -0.7480]]],
# [[[ 0.4746, -1.1667, 0.3207, 0.1962, -2.1549],
# [ 0.4449, -0.3463, 1.5217, -0.6835, 0.6411],
# [ 0.4603, -0.1061, 1.3118, -0.1342, 1.0895],
# [ 0.1289, 0.1187, 1.0467, 0.4937, -1.2150]],
# [[ 0.0758, 0.7100, 1.3112, 0.2789, -0.2307],
# [ 1.6830, -0.4072, 0.5221, -1.1279, 0.5077],
# [ 0.7019, -1.0723, 0.4277, 0.6999, -1.3172],
# [ 0.7492, -0.9616, 1.1176, -0.2311, -0.4924]],
# [[-0.5885, 1.6953, -0.2238, -1.5983, 0.4212],
# [-0.4294, 0.8937, 0.7391, 0.2254, 1.8357],
# [-0.9655, -0.2059, 0.2113, -0.0040, -0.0503],
# [-0.6537, 1.0717, 0.8002, 2.2745, 0.2152]]]])
b = torch.randn(2,3,5,6)
# tensor([[[[-0.7865, 0.6265, 0.4931, 0.9764, 1.8363, -0.8132],
# [-0.3913, 1.6121, 0.8900, 0.6157, -1.0068, 1.5614],
# [ 1.2168, -0.3255, 1.6593, -1.9839, 0.5335, 0.2501],
# [ 0.9769, -0.9781, 0.7857, -1.6423, 1.4239, 0.2151],
# [-0.0949, 0.5603, 0.7432, -0.3031, -0.2769, 0.3482]],
# [[ 0.2275, 0.3536, -0.8794, -0.0094, -0.5691, 0.8944],
# [ 0.9893, 1.0700, 0.4495, -0.8039, 0.2009, 3.1220],
# [-1.0002, -1.0632, -0.8881, -0.3316, 0.3311, -1.1273],
# [ 2.4631, 2.5082, -0.0271, 0.2182, -0.0575, -1.4083],
# [ 0.4188, 0.7744, 0.5722, 0.6768, 0.8458, -1.8130]],
# [[ 2.1234, -0.8771, 1.1661, -0.1264, 0.2965, -0.0036],
# [ 0.0915, 0.9609, -0.7414, 2.0592, 0.3210, -2.0153],
# [ 0.8089, -0.1874, 0.9996, -1.6143, 0.0506, -0.0335],
# [-0.1781, 0.4211, 1.9470, -0.2626, -0.8091, 0.0424],
# [-0.1423, -1.1460, -0.4817, 0.2883, -1.4303, 1.2059]]],
# [[[ 1.7835, 0.3220, 0.0722, -0.1751, -0.1005, 0.4415],
# [ 1.6946, 1.4806, -0.5637, -0.8583, 0.2817, -1.6424],
# [ 0.2370, -0.9394, 1.0580, 0.9210, -1.7519, 0.4598],
# [ 1.9019, 0.2185, -0.8791, 0.7160, -0.5502, -1.1785],
# [-0.7699, -0.8784, -0.5352, -0.4313, -0.1456, -0.0358]],
# [[-1.1553, 0.3783, 0.8394, -0.2807, -0.8861, -0.6191],
# [ 0.2757, -0.2798, 0.2351, 1.4992, -0.5700, 0.2844],
# [-0.2677, -0.8962, -0.0676, -0.2561, 1.1030, -0.7795],
# [ 1.1193, 0.4642, 0.8787, 1.7773, -0.1352, 1.3380],
# [ 0.3299, -1.0302, 1.6842, 0.6148, 0.9973, 0.6206]],
# [[ 0.0878, -0.5342, -1.8645, 0.3344, 0.2799, 0.9512],
# [-0.5912, -0.8268, 0.0946, -1.5592, -1.0715, -0.6558],
# [-0.0135, -0.2939, -1.3945, 0.0041, 1.3270, -0.0122],
# [-0.2027, 0.3042, -0.4048, -1.1073, 0.3252, -1.4158],
# [ 0.1739, -1.5819, 0.4591, -0.0991, -1.5639, 0.1508]]]])
torch.matmul(a,b)
# tensor([[[[ 1.7266e+00, -7.6658e-01, 3.3488e-01, -1.9973e+00, -2.3396e+00,
# 5.0423e-01],
# [ 1.2202e+00, -1.8719e+00, -2.4656e+00, -9.0669e-01, -3.0388e+00,
# 1.7155e+00],
# [-1.6160e+00, 2.7009e+00, 2.1822e+00, 8.9937e-01, 2.8851e-01,
# 6.5878e-02],
# [-7.4547e-01, 7.4572e-02, -1.5743e+00, 1.2832e+00, -1.0526e+00,
# 6.1866e-01]],
# [[-8.6979e-01, -6.4395e-01, -5.2520e-01, 1.6462e+00, -1.7912e+00,
# 1.1687e-02],
# [ 2.0068e+00, 2.1272e+00, 9.1408e-01, -6.9553e-01, 1.2174e+00,
# 4.8225e-01],
# [-1.7905e-01, 2.3493e-01, 1.2445e+00, -6.7741e-01, 6.6092e-01,
# 5.2219e+00],
# [ 6.4473e-01, 7.8646e-01, -2.3582e+00, 6.0144e-01, 3.9146e-01,
# -6.3893e+00]],
# [[-1.6769e+00, 3.6665e+00, -1.0378e+00, 3.7644e+00, 7.0310e-01,
# -4.8402e+00],
# [ 1.6889e+00, 1.0871e+00, 3.5842e+00, -7.6123e-01, 1.2280e+00,
# -1.2806e+00],
# [ 6.1154e-01, 1.1051e+00, -2.1366e+00, 4.9288e-01, 2.6175e+00,
# -2.4028e+00],
# [-2.9488e+00, 1.7845e+00, 2.6418e+00, -1.3886e+00, -9.6650e-01,
# 9.3338e-01]]],
# [[[ 9.7763e-01, 5.9906e-02, 2.0120e+00, 2.2834e+00, -7.3248e-01,
# 2.1190e+00],
# [-1.2262e+00, -2.5114e+00, 2.0951e+00, 8.5488e-01, -2.5253e+00,
# 2.2474e+00],
# [-1.4208e-01, -2.2275e+00, 1.0158e+00, 6.5266e-01, -2.4590e+00,
# 1.0997e+00],
# [ 2.5534e+00, 4.0903e-01, 1.2662e+00, 1.7170e+00, -1.9080e+00,
# -1.9494e-01]],
# [[-6.8757e-03, -9.7798e-01, -1.7148e-03, 1.0611e+00, 7.0653e-01,
# -6.3714e-01],
# [-3.2914e+00, -7.6398e-01, 1.1457e+00, -2.9092e+00, -2.4442e-02,
# -2.7588e+00],
# [-8.7223e-01, 1.8641e+00, -1.2953e+00, -1.4801e+00, -9.4731e-01,
# -9.5393e-01],
# [-1.8510e+00, -4.9159e-02, -7.0515e-01, -2.6517e+00, 6.5704e-01,
# -2.2233e+00]],
# [[-6.5376e-01, -2.1741e+00, 2.4100e+00, -1.1130e+00, -3.4569e+00,
# 6.5767e-01],
# [-3.0246e-01, -3.5620e+00, 6.0591e-01, -1.9654e+00, -2.8945e+00,
# -1.0458e+00],
# [ 2.6153e-02, 7.0223e-01, 1.4646e+00, 8.4549e-03, 3.0804e-01,
# -7.8790e-01],
# [-1.1254e+00, -4.2048e-01, -6.1759e-01, -4.4262e+00, 1.3383e-01,
# -4.5222e+00]]]])
总结
刚一看还挺晕乎,这是干嘛,一个乘法弄得这么复杂。我是这样理解的,其实这里只讲了两件事,一个是乘法,一个是矩阵乘法。两者的区别就在于哪个位置的数据相乘,相乘后的结果是否相加。其他的看着这么乱的主要原因是因为维度和广播。
对位相乘:两个矩阵的元素一一对应相乘,得到一个矩阵。他们的结果不会相加,而且行和列要一致,否则怎么同位运算呢。
矩阵乘法:第一个的行和第二个的列相乘,然后相加。所有这里要求第一个的行的元素个数(列数)要和第二个的列的元素数(行数)一致,否则怎么相乘呢。
维度:因为上面的运算,不管是相乘还是矩阵乘法,都是有维度和形状要求的,其实都是在二维张量上运算,所有超出二维的按批量处理,不够二维的就会考虑广播来补齐。
广播:广播就是将一个张量补齐到另一个张量的维度,然后进行运算。
这样是不是好理解多了,我们再来理解一下上面的几个操作(*、 mul()、multiply()、mm()、bmm()、mv()、dot()、matmul()、@):
*、 mul()、multiply():就是对应位相乘,得到一个张量。但是当其中一个是标量的时候,就会广播。mm()、bmm(): 矩阵乘法,他们其实都是用行和列相乘再加和。当维度超过二维就会按照批量来处理,当维度不符合要求就会用广播方式补齐。mv()、dot():这两个有点特殊,他们第二个参数都是向量,如果非要向矩阵乘法上靠,那就只能理解为第二个参数扩展为列也就是shpae(n,1)形状。这地方是我的理解,如果有问题,欢迎指正。有明白的也可以评论区留言。matmul 、@:mm()、bmm()、mv()、dot()的集合体,为啥说mv()、dot()要向矩阵乘法靠,也是出于这个原因。另外在
mm()、bmm()、mv()、dot()中都有提到不广播,这个不广播和上面的广播不冲突,因为调用这几个方法的时候,你传入的维度不够,他是不会帮你广播的。但是matmul 、@在处理的时候就会广播。